After a few hours of blind coding I realized that, not having taken any computer algorithm-related courses at uni, nor ever having played with artificial intelligence or game strategic mechanics, this would turn out to be quite the challenge. Still, blinded by how hard can it be?, I set about writing an AI which would solve this game consistently better than I could. It was obvious that people had come up with near-perfect strategies for solving the game, but I decided not to investigate those and rather try to figure it out myself. I also decided to avoid any "if this configuration exists, do that"-solutions into the algorithm -- the program was to be entirely autonomous in that respect. I reckoned something like this would be a good start:
Implementation of the above algorithm was fairly straight-forward. The challenging part is the
assessment of a board
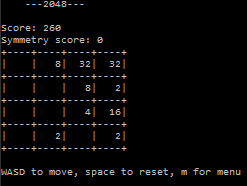
configuration. What makes a good board? Is symmetry of tiles more important than a large increase in
score? Should
priorities stay the same throughout the course of a game? Not being very good at this game myself,
these questions
were difficult to answer. At this stage the game pretty much runs itself, and all I can really do is
fiddle with the
following constants until I hit the jackpot:
cornerAWnot in usecornerWeighthow much to favor large tiles in cornersymmetryWeighthow much to favor symmetry on boardemptyCornerPenaltyhow much to penalize empty cornersfewerTileWeighthow much to prioritize tile reductionrecursionDepthhow many layers of recursionscoreWeighthow much to weight increase in score
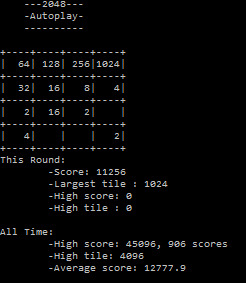
The values which are set in the downloadable code below is ones which I have had the most success with. The current high-score for my AI is currently 45,096 with the largest tile being 4096.
I later made an attempt at writing an algorithm which learned what combinations of these coefficients gave the best results, but this proved unfruitful. I may return to this project and try to achieve a higher score some day.